基本信号模式与表示法

前言

在计算机模型中，将现实世界的信号高效地表示为数据对于模型的性能至关重要。如果信号表示包含不必要的细节，模型的计算效率就会降低；如果表示过于抽象，模型就无法预测重要的现象，或者给出不准确的结果。根据要解决的问题，可以选择合适的信号表示模型。

先解释一下基带、频带、宽带和带宽：

基带（Baseband）也叫做基本频带，指的是未经调制的原始信号（数字信号）所占的频带（Frequency Band）；
频带（Frequency Band），指的是信号所占用的频率范围。对信号做频谱变换后，频谱最低频率到最高频率之间的范围；
宽带（Broadband），指的是容许多个不同频带的信号在同一个信道上。例如频分、波分复用，将信道分成多个子信道，分别传送音频、视频信号，称为宽带传输（传输模拟信号）；
带宽指的是频谱能量集中的某段频带的宽度。

光信号

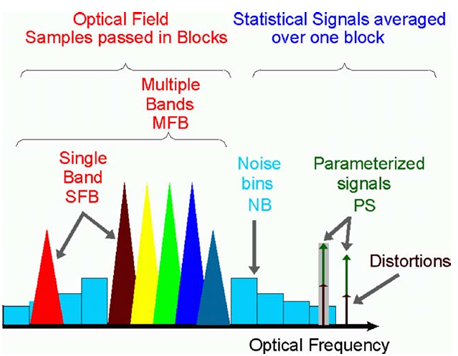
VPI光学系统提供两种信号模式：块模式和采样模式。这些模式定义了数据在模块之间传递的方式。当数据单向传递或在间隔较大的组件之间传递且时间延迟远大于数据块的持续时间时，使用块模式。通常每个数据块代表数十到数千个数据位。单频带（Single Bands）是最通用的一种，新用户应默认使用SFB表示光信号。

单频带（SFB）

单频带（SFB）是最通用的块模式信号表示形式，构成了大多数模拟的基础。对光纤进行的单频带模拟将涵盖所有四波混频效应以及噪声与信号的相互作用。然而，通过将单频带与其他块模式信号格式结合使用，可以实现更高的效率，这会在后面进行讨论。

创建单频段

除了专门设计用于采样模式的信号源和多波长信号源之外，大多数信号源都会产生SFB 信号。若要强制信号源产生 SFB 信号，在信号源处将OutputDataType设置为BLOCKS。

当多个源合并时，各个源的采样率应大于信号之间的频率间隔。这样可以确保信号自动合并为单个频段，而不是作为多个频段（MFB）单独传播。需要注意的是，在重叠的频率区域内，只有一个频段应具有较大的信号功率，因为信号的相位可能会导致相长或相消干涉。如果两个或多个 MFB 重叠，它们将自动转换为单个频段（SFB）。

案例： Optical Systems Demos > Simulation Techniques > General > Creating SFB and MFBs

SFBs的数学基础

以下部分介绍了将光信号表示为采样波形的数学基础

基带变换

对于调制光波而言，调制频率总是远低于光载波频率。因此，光波的调制信息和载波光场可以相互独立地加以考虑。由此，光学系统可以在基带中建模，即光载波频率与信号分离，并被视为一个常数参数。剩下的信号仅由光场的时间相关复振幅包络构成。

光信号的载波频率称为参考频率，用 $f_c$ 表示。它通常由光源的发射频率决定。基带频谱是通过将调制频谱移至直流附近而生成的。因此，基带频谱通常在直流附近不对称。这意味着适当的时间函数必须是复值的，以便正频率和负频率相互独立。

复振幅表征

从数学角度来看，基带信号变换对应于慢变振幅近似法。当 $\widetilde{E}(t)$ 表示电场的实部时，有

$\widetilde{E}=E(t)\exp(j2\pi f_ct)+c.c.\tag{1}$

其中 $E(t)$ 为载波频率为 $f_c$ 的光波的复振幅。 $c.c.$ 表示前一项的复共轭（complex conjugation）。假设调制频率远低于光载波的振荡频率，这表明

$\left| \frac{1}{E}\frac{dE}{dt} \right|\ll f_c\tag{2}$

（1）（2）式极大简化了光学元件的建模。这是通过用仅考虑复振幅 $E(t)$ 的方法取代基于麦克斯韦方程组求解的方法（后者需要巨大的仿真带宽）来实现的，而不再考虑总光场 $\widetilde{E}(t)$ .

根据上两式的简化，在频域中考虑的基带变换变得简单明了。域间的转换可通过傅里叶变换来实现：

$\begin{aligned} Y(f)&=\int_{-\infty}^{\infty}X(t)e^{-j2\pi ft}dt\\ X(t)&=\int_{-\infty}^{\infty}Y(f)e^{j2\pi ft}dt\\ \end{aligned}\tag{3}$

其中 $X(t)$ 是时域中的信号， $Y(f)$ 是频域中的信号。傅里叶变换的一个已知特性是，频谱 $Y(f)$ 在频率值 $f_0$ 处的偏移会导致时域信号 $X(t)$ 乘以相位项 $\exp(j2πf_0t)$ 。换句话说， $X(t)\exp(j2πf_0t)$ 的傅里叶变换给出 $Y(f - f_0)$ 。因此， $E_\mathrm{base}(t)$ 和 $E(t)$ 的频谱之间仅存在简单的频率偏移关系，其值等于信号的载波频率。这证明了基带变换和慢变振幅法的等效性。

光的偏振表示

由于在光通信系统中，光通常以非偏振态传播，从而导致偏振模色散。VPI通过在所有块和样本模式的模拟中传播两个正交偏振态来处理偏振效应。

到目前为止，我们一直将电场视为标量，并忽略了其偏振态（State Of Polarization：SOP）。通常，电场是一个三维矢量 $E(t) = \{E_x(t), E_y(t), E_z(t)\}$ 。在自由空间中，该矢量始终与传播方向垂直，假设传播方向沿 z 轴。因此，电场的振荡始终是横向的，即 $E_z(t) = 0$ 。在光通信技术中，光波通常在波导中传播，一般不是横向的。然而，如果我们不讨论光波模式特性的细节，而首先关注信号的时间行为，那么只考虑电场的横向分量是一个很好的近似。

$E(t)=\{ E_x(t),E_y(t) \}\tag{4}$

这种近似在弱导波结构（傍轴近似）中尤其有效，此时 $E_z(t)$ 远弱于 $E_{x,y}(t)$ 。在对强导波结构建模时，如果不能忽略 $E_z$ 分量，则应根据麦克斯韦方程组从 $E_{x,y}$ 分量计算出 $E_z$ 分量，因为这三个分量之间存在关联。

琼斯矢量（Jones Vector）

矢量 $\{ E_x(t),E_y(t) \}$ 通常被称为琼斯矢量，它明确定义了光在任何时刻的偏振态。VPI中琼斯矢量用于描述单频带信号的偏振态。对于给定的时刻 $t$ ，此矢量可以表示为

$\{E_x,E_y\}=E\{\sqrt{1-\kappa},\sqrt{\kappa}\exp(j\delta)\}\tag{5}$

其中 $E$ 是复振幅， $\kappa$ 是功率分配比， $\delta$ 是 $E_x$ 分量和 $E_y$ 分量之间的相位差，即 $\delta=\arg(E_y)-\arg(E_x)$ 。对于右旋圆偏振， $E_x$ 滞后于 $E_y$ ，且 $0\lt\delta\lt\pi$ 。

斯托克斯矢量（Stokes Vector）

另一种对偏振态的常规描述是基于斯托克斯矢量的。尽管斯托克斯矢量不用于SFB 信号的表示，但它们用于其他类型的信号。因此，这里说明斯托克斯矢量与琼斯矢量之间的关系是有用的。“瞬时”斯托克斯矢量定义为

$S(t)=\{S_0(t),S_1(t),S_2(t),S_3(t)\}\tag{6}$

斯托克斯矢量的各分量之间存在如下关系：

$\left\{ \begin{aligned} S_0(t)&=|E_x(t)|^2+|E_y(t)|^2\\ S_1(t)&=|E_x(t)|^2-|E_y(t)|^2\\ S_2(t)&=E_x(t)E_y^*(t)+E_y(t)E_x^*(t)\\ S_3(t)&=j\{E_x(t)E_y^*(t)-E_y(t)E_x^*(t)\} \end{aligned}\tag{7} \right.$

并且

$S_0^2(t)=S_1^2(t)+S_2^2(t)+S_3^2(t)\tag{8}$

这些分量具有如下含义：

$S_0$ 是总光强（总平均功率）
$S_1$ 是水平偏振分量与垂直偏振分量强度之差。当 $S_1$ 为正值时，表明更倾向于水平偏振；当 $S_1$ 为负值时，则表明更倾向于垂直偏振。
$S_2$ 表示对+45°或-45°线偏振方向的偏好。 $S_2$ 为正值意味着更倾向于+45°线偏振。
$S_3$ 表示对左旋圆偏振或右旋圆偏振的偏好。 $S_3$ 为正值意味着更倾向于右旋圆偏振。

根据（6）式，斯托克斯矢量和偏振态可能发生非常迅速的变化或波动。正因如此，计算时间平均偏振态往往很有意义，这可以通过TC Modules > Instrumentation > ExtractSOP模块来实现。斯托克斯矢量的分量可以在感兴趣的时长内进行平均：

$S_i=\left<S_i(t)\right>\qquad i=0,1,2,3\tag{9}$

在ExtractSOP模块中，平均值是针对整个模拟时间窗口计算得出的，该时间窗口是为每个模拟全局定义的。斯托克斯矢量的第一个分量代表信号的总平均功率（包括两个偏振态）。我们采用一种约定，即其他分量相对于 $S_0$ 进行归一化，即

$s_i=\frac{S_i}{S_0}\qquad i=0,1,2,3\tag{10}$

对于平均矢量而言，式（8）不再普遍成立。该比值

$p=\frac{\sqrt{S_1^2+S_2^2+S_3^2}}{S_0}\qquad 0\le p\le1\tag{11}$

定义了光的偏振度。对于其偏振态不随时间变化的信号，偏振度为 100%，且式（8）成立。这些信号被称为完全偏振。偏振干扰会使偏振随时间旋转，从而降低 p 值。

用式（5）中定义的琼斯矢量的参数来表示斯托克斯矢量的各分量，则有

$\left\{ \begin{aligned} s_0&\equiv1\\ s_1&=1-2\kappa\\ s_2&=2\sqrt{\kappa(1-\kappa)}\cos\delta\\ s_3&=2\sqrt{\kappa(1-\kappa)}\sin\delta \end{aligned} \right.\tag{12}$

庞加莱球面（Poincare Sphere）

从几何角度式（11）来看，对于完全偏振光，各种偏振态（SOP）可以映射到一个偏振球的表面上，即所谓的庞加莱球。如果偏振度小于 1，则偏振态映射到庞加莱球内部的一个点上。球的半径由 $S_0$ 定义。赤道代表各种形式的线性偏振。右旋和左旋圆偏振态位于球的两极。其他点代表椭圆偏振光，其中右旋椭圆偏振态位于北半球，左旋椭圆偏振态位于南半球。通过球心的直线两端的点代表正交偏振。

偏振椭圆（Polarization Ellipse）

根据琼斯矢量，有

$\frac{E_x^2}{E^2}+\frac{E_y^2}{E^2\cdot\exp(2j\delta)}=1\tag{13}$

对于完全偏振光，任意偏振态也可以用偏振椭圆来表示。椭圆度 $\varepsilon$ 描述了椭圆半轴的长度比。如果 $\varepsilon$ 很小，椭圆就变得扁长：如果它接近于零，偏振就是线性的。如果 $\varepsilon$ = ±45°，偏振就是圆偏振。右旋椭圆和左旋椭圆的偏振态分别由正的和负的 $\varepsilon$ 来描述。第二个参数是方位角 $\eta$ 。它表示椭圆长轴相对于 $E_x$ 轴的取向角。

偏振椭圆参数与式（5）中的方位角 $\delta$ 的关系为：

$\begin{aligned} \tan2\eta&=2\frac{\sqrt{\kappa(1-\kappa)}\cos\delta}{1-2\kappa}\\ \sin{2\varepsilon}&=2\sqrt{\kappa(1-\kappa)}\sin{\delta} \end{aligned}\tag{14}$

将斯托克斯矢量与偏振椭圆的参数联系起来也是很有用的：

$\left\{ \begin{aligned} s_1&=\cos2\eta\cos2\varepsilon\\ s_2&=\sin2\eta\cos2\varepsilon\\ s_3&=\sin2\varepsilon \end{aligned} \right.\tag{15}$

根据（14）式，方位角和椭圆度可以被解释为庞加莱球面上的角。下图展示了偏振椭圆与庞加莱球之间的关系。

演化方程：光纤模型

在提取载波频率并将信号转换为基带之后，提取出的载波频率与复包络一起作为单个常数（边界参数）传递。只要实际信号的带宽小于仿真带宽，这种信号表示形式就与物理信号包含相同的信息。通常，光信号在衰减介质中的演化，其中线性和非线性效应会影响传输信号，可从数学上表示为

$\frac{\partial}{\partial z}E=\{\hat{D}+\hat{N}-\hat{\alpha}\}E\tag{16}$

其中 $\hat{D}$ 表示线性算符， $\hat{N}$ 表示非线性算符， $\hat{\alpha}$ 表示介质的衰减算符。当对光纤进行研究时， $\hat{D}$ 对应传输光的色散效应， $\hat\alpha$ 对应光线衰减。 $\hat N$ 描述了包括自相位调制（SPM）和交叉相位调制（XPM）、四波混频（FWM）以及拉曼散射在内的效应。

离散转换

通常，光波的复包络可以用在时间和频率上都是连续的波形来描述。然而，这种表示法必须进行近似处理，因为连续信号无法通过本质上是离散的数字计算来处理。

离散时间转换

将连续时间域的描述转换为离散时间域的描述意味着只在连续时间轴上的离散点处考虑波形。为了便于计算，这些点在时间上是等间距分布的。这种转换称为采样，而采集时间样本的速率称为采样率，用 $f_s$ 表示。

在采样系统中，连续的时间轴被离散的时间网格所取代，即 $t = n\Delta t$ ，其中 $n = 0,1,...$ 。相邻样本之间的间隔称为采样间隔（或时间步长）。采样间隔 $\Delta t$ 与采样率 $f_s$ 之间满足 $\Delta t=(1/f_s)$ 。在VPI中，源被设置为在该时间网格上生成样本，并且通常会避免导致样本点不在时间网格上的延迟，或者将其实现为频率相关的相移。因此，除了限制可模拟的带宽之外，周期采样本身并不会造成近似。

下图展示了时域和频域中的采样过程，并说明了采样间隔与仿真带宽之间的重要关系。对于波分复用（WDM）系统而言，仿真带宽必须涵盖所有信道（除非使用多个频段）。较宽的仿真带宽需要较短的采样间隔：通过选择每个符号或脉冲有较多的采样点来获得较短的采样间隔。

从离散时间域到离散频率域的转换是通过离散傅里叶变换（DFT）来实现的。快速傅里叶变换（FFT）是 DFT 的一种高效实现方式。由于高效转换是仿真同时具有时变非线性以及频变相位和振幅操作的光学系统的关键，因此该工具采用了非常高效的 FFT 实现方式。

对时域表示进行采样会导致频率响应的周期性扩展。也就是说，频谱会以等于采样频率的周期重复出现。在物理系统中，可以通过带通滤波（低通滤波可在基带恢复，而带通滤波可在接近原始载波频率处恢复）来恢复感兴趣的频率区域。因此，具有适当带宽的带通滤波是时域采样的逆操作。实现这一操作的条件是信号带宽小于频域中的重复周期（采样定理，奈奎斯特频率大于基带带宽一半），即采样率 $f_s$ 。否则，会发生混叠误差，这是由于频谱周期性扩展时出现重叠所致。然而，在仿真中，相当于带通滤波的做法是仅显示周期性频谱的一个周期。仿真的采样波形输出永远不会转换回连续波形。

在仿真中，让光源仅产生处于模拟光带宽内的信号是很容易做到的，从而避免混叠现象。然而，要让频率混频（例如由于光纤非线性）的产物也保持在该带宽内却并非易事，除非模拟带宽是原始信号带宽的数倍。在这种情况下，混叠会导致生成的超出模拟带宽的频率分量被折回到模拟带宽内。实际上，这些分量的频率会偏移 $nf_c$ ，其中 $n$ 是一个整数，使得信号被重新映射回模拟带宽内。

Nyquist-Shannon（奈奎斯特-香农）采样定理告诉我们，当

$f_s\ge B_{max}\tag{17}$

即采样率 $f_s$ 大于等于连续时间波形的带宽 $B_{max}$ 时，实数域连续时间波形可以转换为采样的复基带形式而不丢失信息。采样率 $f_s$ 为两倍奈奎斯特频率 $f_{N}$ 。

离散频率转换

与时域采样类似，可以想象频域中的采样过程。若仿真时间窗口越大则频域采样越精确，这是因为在一个有限时间窗口内表示的信号将具有有限的频谱分辨率，该分辨率等于窗口持续时间的倒数。VPI可以生成比表示此分辨率所需的频率点更多的频率点（使用基于正弦和余弦的离散傅里叶变换），但这很浪费计算资源，大多数快速傅里叶变换技术仅生成恰好能表示频率分辨率的频率点。

为了在傅里叶变换期间避免频点之间出现泄漏（这会降低频谱的精度，尤其是在接近激光峰值时），时间波形必须在时间窗口内是周期性的（时间分辨率处处相等）。如果发射机只是一个正弦余弦发生器的话，很容易实现所有发射器都锁定在等于频谱分辨率的频率网格上。在这种情况下，时域和频域之间的转换是精确的，无需近似处理即可完成。

对于数字传输，仿真时间窗口的长度可以用符号数 $N_s$ 乘以符号持续时间 $T_s$ 来表示，而 $T_s$ 是符号率 $r_s$ 的倒数。频率或频谱分辨率，即频域中的采样周期，则为 $r_s/N_s$ 。因此，通过增加符号数，从而增加模拟时间窗口，可以提高频谱分辨率。

SFB 格式的优势与劣势

对于大多数应用而言，将光波描述为采样的单频带是最准确的方法。如果模拟带宽足够宽，则会自动考虑光纤链路设计中的所有重要特性，例如四波混频、拉曼散射和色散。对于单频带表示的信号，演化方程（16）形式特别简单，耦合项会自动包含在内，因此所研究的光学组件和网络元件的建模算法相对容易实现。

SFB 信号的缺点在于其对内存和计算能力的要求较高；尤其是在长时间（例如多个符号）内对宽带信号（例如多个 WDM 信道）进行研究时。例如，由于放大自发辐射（ASE）的带宽超过 10 THz，因此很难将其完整的噪声带宽考虑在内。因此，VPI开发了近似噪声频谱的方法，并在噪声箱的形式下进行研究。

电信号

通常，系统级光子设计工具的任务之一是研究整个系统中的信号传输情况。这包括对发射端调制电流以及电接收端电压的描述。在VPI中，电信号有其自身的表示形式，这与光信号描述相互独立，从而能够区分光数据信号和电数据信号，防止光端口与电端口的不物理连接。

电学信号的表示方式类似于光信号的单频带（SFB）描述：电学信号通过单一采样频带来表示。与光波的描述不同，电信号无需考虑偏振，也不必进行基带变换，因为电学信号的频率范围远低于光波的载波频率，即使载波是微波，也能在基带有效地表示。这是因为采样率由光信号决定，远高于电学信号所需的采样率。因此，光学组件占据了系统计算工作的大部分，所以电学模拟的效率提升影响甚微。直接表示电信号本身而非其复包络意味着它是用实值信号来描述的。电信号以“幅度”单位来处理，这可能对应于安培或伏特。

对时域中的实值信号进行傅里叶变换会得到一个以直流分量为中心的对称频谱。电学信号通常不考虑这种双边频谱，而是采用等效的单边频谱描述。当 $\hat P(f)$ 定义了一个双边对称频谱时，其等效的单边频谱 $P(f)$ 可以表示为

$P(f)= \left\{ \begin{aligned} \hat P(f)&,\qquad f=0\\ 2\hat P(f)&,\qquad f>0 \end{aligned} \right.\tag{18}$

对于从连续续波形到离散信号表示的转换，正如在 SFB 中所述，同样的性质也适用。由于只需考虑实值时间信号，这简化了转换过程。

逻辑信息

除了物理信道信息之外，在模型之间交换有关传输信号特性的信息也非常有用，例如比特序列和原始脉冲形状。这种所谓的逻辑信息附加在物理信号上，并且可以通过指定其唯一的标签和索引，由模拟传输链路的所有模型访问。一个典型的应用是通过误码率（BER）估计器提取比特序列。可以通过使用全局仿真参数LogicalInformation来设置逻辑信息的跟踪。

块模式下的逻辑信息

逻辑信息的添加

每个生成信号的模块都会向信号添加一个新的逻辑信息集。这个集合被称为“逻辑通道”。逻辑通道通过通道标签和通道索引进行标识。该集合的标签要么从模块的实例名称派生而来，要么通过参数 ChannelLabel 进行设置。通道索引用于区分多次连续的运行操作。光信号或电信号的源使用 AddLogicalInfo 参数。此参数与全局参数 LogicalInformation 一起定义模块是否生成逻辑信息。如果 AddLogicalInfo 和 LogicalInformation 均设置为 On，则会创建带有所有相应逻辑信息的逻辑通道。如果 AddLogicalInfo = On 且 LogicalInformation = Off，则会创建一个带有指定标签的空逻辑通道，其中不包含任何逻辑信息。例如，模块 TestSetAmplifier 可以使用这样的通道来选择用于分析的必要信号。

除了光信号和电信号的源之外，逻辑信息由调制器添加。调制器并非像源（载波信号和脉冲形成器）那样创建新的逻辑信道，而是将与调制信号相关的逻辑信道的参考信息插入到与载波信号相关的逻辑信道中。此类参考信息包含调制信号的标签、调制比特率和调制类型。

需要有关信号信息的模块（例如，BER模块需要已传输的比特流和比特率）可以通过指定逻辑信道的标签和索引（参数 ChannelLabel 和 ChannelIndex）来访问在传输期间添加到信号中的所有逻辑信道。当单通道发射机传输一系列块（进行多次迭代）时，它会生成具有特定 ChannelLabel 的一个逻辑信道。为了区分发射机的不同发射，会在 ChannelLabel 后添加一个索引。索引从零开始，并在每次块迭代时递增。如果原理图中没有循环，接收机将仅接收来自单个发射机的块，此时无需索引。将参数 ChannelIndex 设置为 -1 可告知接收机在每次迭代中使用找到的最高索引。

如果存在环路（或其他叠加情况），接收机会遇到一个信号，其中来自同一发射机的多个逻辑信道块同时出现，这些块仅通过各自的索引加以区分（将两个信号相加总是会将逻辑信道集相加）。ChannelIndex 可让用户明确选择用于生成参考信号的逻辑信道块的索引；如果为正数，则接收机模块将使用给定索引的信道来恢复接收到的第一个块的时钟，并随后递增索引；如果为负数，则接收器将始终使用找到的倒数第 N 个索引。

提高误码率（BER）估计精度的一种常见方法是将多个块信号的数据进行累加（包括蒙特卡罗技术）。特别是对于长比特序列，这可能会导致内存消耗过大（与信号不同，逻辑信道在接收后不会被删除）。通过将全局参数 LogicalInformation 设置为 CurrentRun，可以避免这种情况，这会强制仿真引擎在开始下一次运行前重置所有逻辑信道。

需要注意的是，在复杂网络的模拟中，有时需要在仿真拓扑结构中添加逻辑延迟。若添加了逻辑延迟，多次运行操作生成的信号可在仿真中同时存在，此时将 LogicalInformation 设置为 CurrentRun 将会导致错误。在这些情况下，使用 LogicAddChannel 模块并将 LogicalChannelMode 设置为 Delete，同时为 ChannelIndex 参数设置合适的值可能会有所帮助。

逻辑传输链路示例

典型的传输链路以如下方式访问逻辑信息库：

执行行编码和脉冲成形任务的模块会对生成的比特流进行处理，通过向信号添加逻辑信息集来传递信息（例如比特流、比特率和脉冲形状）。默认情况下，此信息集会根据模块的实例名称进行标记，或者用户也可以通过设置 ChannelLabel 参数来进行设置。
例如，一个光源（如激光器）定义了所传输块的参考频率和带宽，并添加了一个包含此信息的逻辑信息集。
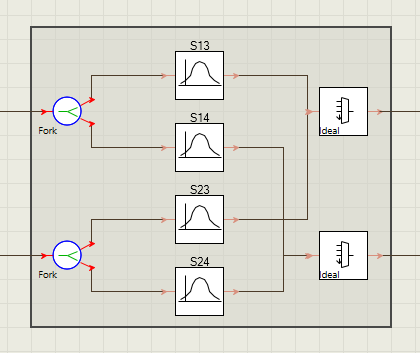
调制器向与调制信号相关的逻辑信道添加信息。这些信息包括由上图中标记为“脉冲成形器”的编码器生成的逻辑信道的调制格式、比特率和标签。由载波信号源生成的逻辑信道（Ch.1）包含对由脉冲成形器生成的逻辑信道（Ch.2）的引用参考。
执行时钟恢复的模块需要有关比特流、比特率和脉冲形状的信息，以生成新的、未受干扰的脉冲流。模块所使用的逻辑信息集可通过参数 ChannelLabel 和 ChannelIndex 进行指定。然后，通过与接收到的波形进行相关性分析来找到最佳的时钟相位。
BER模块需要有关传输比特流的信息，以便将其与接收到的信号进行比较。用于此目的的逻辑信息集同样可以通过参数 ChannelLabel（信道标签）和 ChannelIndex（信道索引）来指定。

样本模式下的逻辑信息

为避免在块与块之间传递单个样本时产生开销，在样本模式下不会生成逻辑信息。处于采样模式的发射机不会将其逻辑信息集添加到输出信号中。接收机所需的逻辑信息可以使用 LogicAddChannel 模块附加到块信号上。块信号由 SampleToBlock 模块生成，该模块用于将采样模式信号转换为块模式信号。