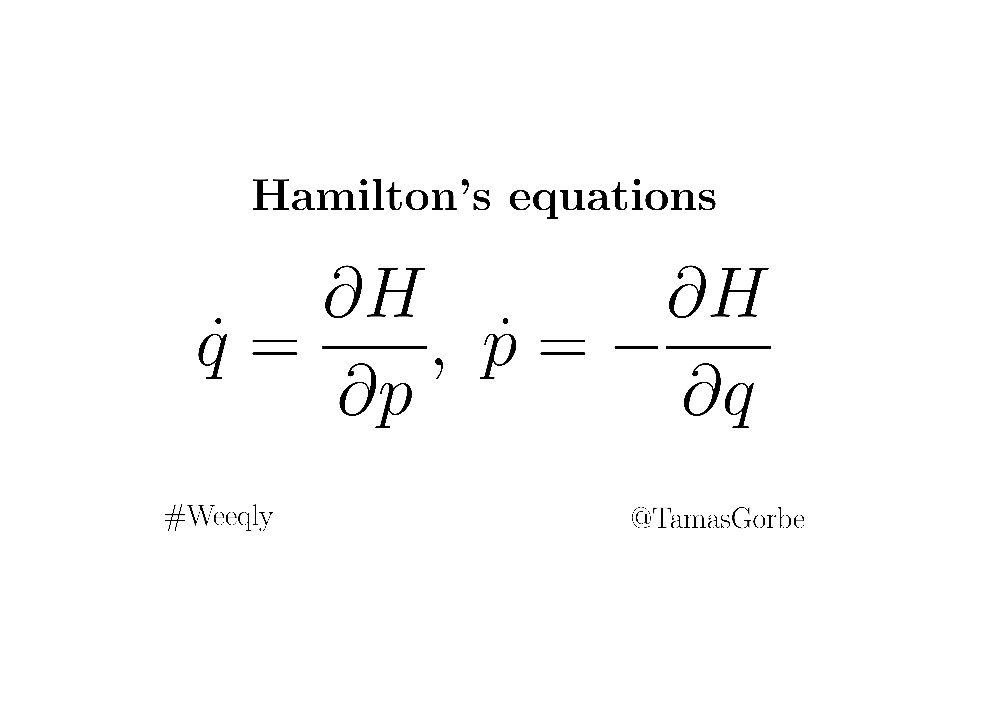哈密顿原理和费马原理

哈密顿原理

哈密顿原理也叫最小作用量原理。爱尔兰数学家威廉·哈密顿认为，要求经典力学系统的演化（位形空间中的轨迹），除了通过牛顿三定律，也可以通过求作用量 $S$ 的极值得出，该原理叫做哈密顿原理，作用量 $S$ 可以表示为

其中 $L$ 是拉格朗日方程，经典物理学里的意义是系统总能量（动能与势能之和）

$L(x,y,z,\dot{x},\dot{y},\dot{z})=T-V=\frac{1}{2}m(\dot{x}^2+\dot{y}^2+\dot{z}^2)-V(x,y,z,t)$

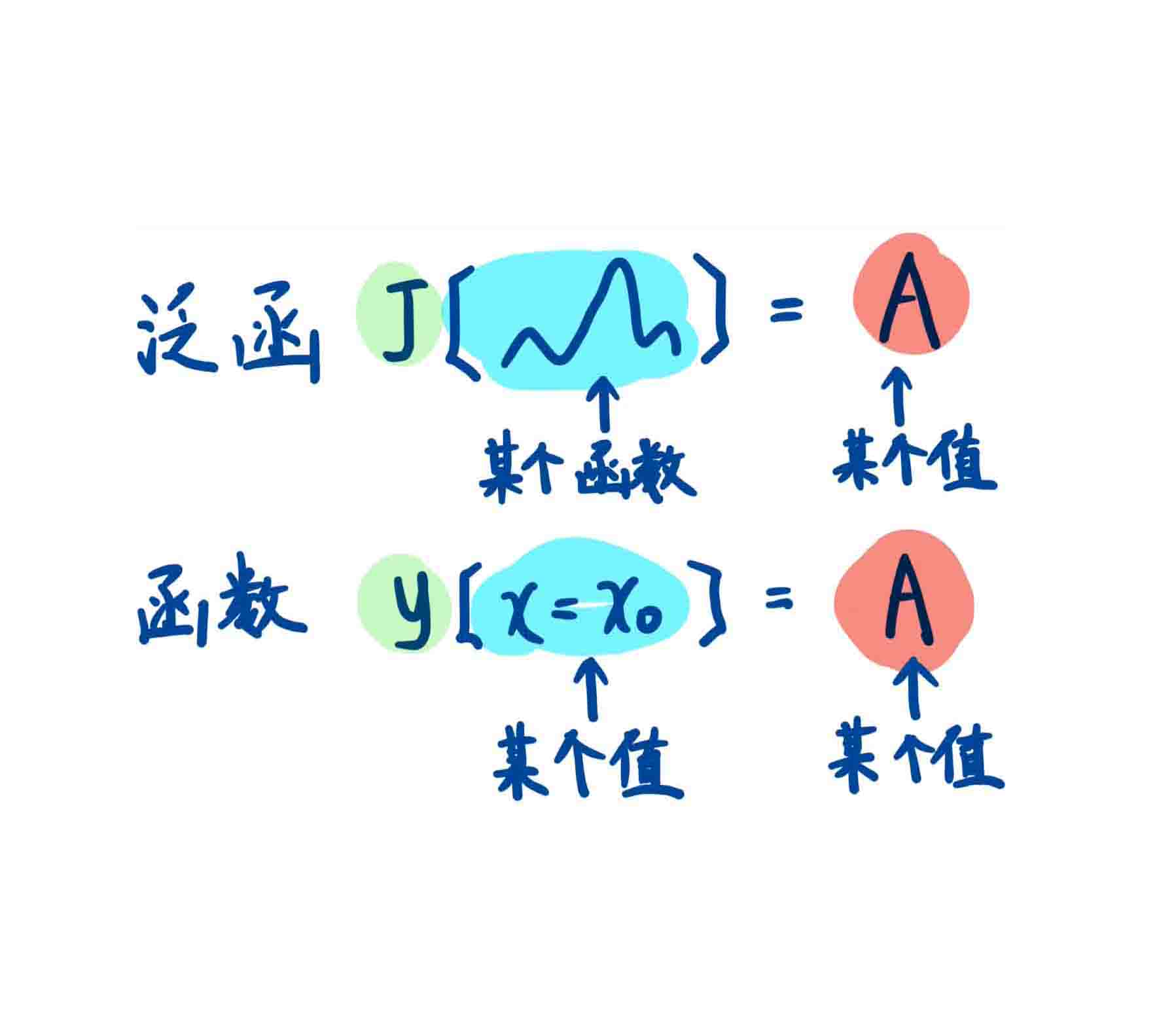
作用量 $S$ 的函数值是一个实数，但自变量是N个实函数，因此 $S$ 为一个泛函。

哈密顿原理的物理图像即能量的演化规律：系统能量会朝着平稳的状态发展（可能是极小，极大或稳定值）。

根据哈密顿原理，可以推导出拉格朗日方程满足方程组：

拉格朗日方程组的物理意义是动量守恒（牛顿第二定律的分量表示）。当系统无外界影响时，系统自身从某个状态转变为另一状态时满足系统动量守恒。

数学形式：

结合拉格朗日函数，我们定义光学拉格朗日量为：

对应光学拉格朗日方程组：

将拉格朗日量带入拉格朗日方程组，并根据 $ds=(1+\dot{x}^2+\dot{y}^2)^{1/2}dz$ ，可以得到光学程函方程：

当应用傍轴近似时：

该方程即为几何光学里的傍轴近似射线方程。

对光学程函方程的讨论：

光学里的牛顿第二定律
本质是光学里动量守恒的体现（光学中时空度量等价， $ds=\frac{c}{n}dt=\frac{1/\sqrt{\epsilon_0\mu_0}}{\sqrt{\epsilon_r\mu_r}}dt=\frac{dt}{\sqrt{\epsilon_0\epsilon_r\mu_o\mu_r}}=\frac{dt}{\sqrt{\epsilon\mu}}$ ， $\epsilon$ 和 $\mu$ 为材料的介电常数和磁导率，是材料自身的属性），光学动量的改变率等于场势能提供的力
光学方向余弦的变化率与折射率分布的梯度成正比，光会朝着折射率变大的方向靠近传播，折射率梯度越大的地方对光场约束能力越强