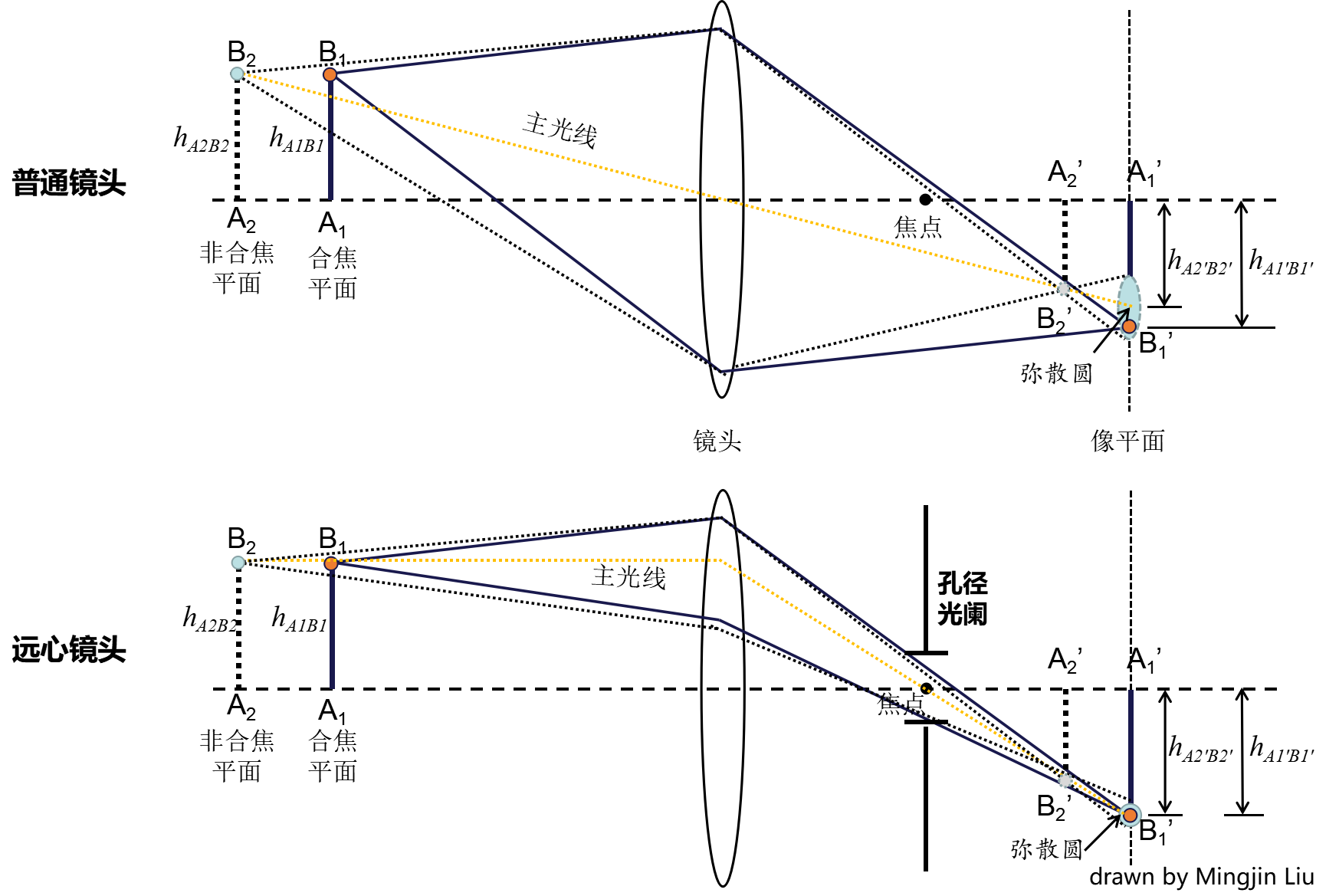
赛德尔像差理论

球差演化

前提假设

基于高斯光学下的拓展，任意一束光线都可以由两个特殊光线进行线性叠加来表示，折射面可以表示为一个光线传输矩阵（ABCD矩阵），该矩阵对光线做的是线性变换。

图 1. 两条特殊的近轴光线

这两条特殊的近轴光线可以看成射线空间里的两个独立但不正交的维度。在理论力学中描述一根光线的自由度有两个，位置和方向，即光线从哪儿射出的，光学方向余弦是多少，这对应着理论力学中广义坐标和广义动量。对于这个限制在子午面的光学系统，给出了两个广义坐标即两条特殊光线，刚好等于系统的自由度，因此这个系统是一个完整约束系统，系统内所有光线都能够用这两条光线的线性叠加来表示。

图 2. 传输矩阵
  1. 既然该系统是一个线性系统，那么系统内所有的参量都可以通过线性矩阵的形式表示出来。输入光线用位置和角度表示成一个向量，薄透镜用光线传输矩阵，也就是Zemax里的ABCD矩阵表示，则输出光线为上面两个矩阵的乘积。
  2. 从哈密顿光学理论中我们得知，三阶像差是求解光学哈密顿方程时保留一阶和三阶泰勒展开相对于仅保留一阶泰勒展开（高斯光学）的偏差值。基于泰勒展开的思想，我们可以认为当系统微弱偏离线性系统后，可以看成是原线性系统与某个非线性系统，例如三阶非线性系统的叠加。
  3. 基于高斯光学的拓展下，三阶像差经过三阶非线性系统可以看成三阶像差先经过一个线性变换，再与该三阶非线性系统产生的非线性微扰进行叠加。

球差经过单折射面后的变化

图 3. 球差经过单个折射面后的变化

高斯光学下上图折射面不会引入像差，在对高斯光学拓展后，该折射面偏离了一阶线性系统，附加了三阶非线性，产生了球差。物方若存在球差，则像方得到的球差根据前面的理论解释，可以表示成物方球差乘以一个转面倍率再加上该折射面自身产生的球差，表示为

{δL′=αδL+δL∗α=nusin⁡Un′u′sin⁡U′(1)\left\{ \begin{aligned} \delta L'&=\alpha\delta L+\delta L^*\\ \alpha&=\frac{nu\sin U}{n'u'\sin U'} \end{aligned} \right.\tag{1}

  1. 这里转面倍率α\alpha的由来是将轴向放大倍率里u2u^2的一个uu替换为sin⁡U\sin U。原本的轴向放大倍率为α=nu2n′u′2\alpha=\frac{nu^2}{n'u'^2}，该式可以在高斯条件下变形拉格朗日不变量得到。球差的大小是随着孔径变化而变化的，也就是与离轴光束的倾角有关，那为什么不用UU而用sin⁡U\sin U呢？因为对于离轴倾角较大的光线，横向放大倍率不再能够从拉格朗日不变量中得到，而是从正弦条件中得到。纵向放大倍率从正比于近轴放大倍率的平方变为正比于近轴放大倍率乘以满足正弦条件的离轴放大倍率。
  2. 将正弦的泰勒级数展开，一阶后便是三阶，说明对于离轴光线在保留高斯光学的系统上拓展了三阶非线性。这里之所以是近轴放大倍率乘以满足正弦条件的离轴放大倍率，是因为系统要满足高斯光学到三阶像差拓展光学的平稳过渡。既包含近轴的形式，又包含拓展的高阶非线性项。
  3. 从本质上看，这里转面倍率中的uu写成sin⁡U\sin U也好，写成u+u3u+u^3也罢，本质是为了体现出折射界面偏离一阶形式的高阶项，剩余的量会以折射面自身产生球差的形式包含在内，不用过度理解其物理意义。高阶像差的本质是理论计算与实际结果之间的偏差，理论计算的方式是以类似微扰法的形式进行泰勒展开计算，而像差的泰勒展开为一个无穷级数，因此对于高阶像差讨论其物理图像没有意义。

单个折射面的球差贡献

系统球差可以看成系统内所有单折射面贡献的一份一份球差之和，这部分球差体现在式（1）的δL∗\delta L^*里，因此定义单个折射面球差贡献量为

−12SI=n′u′sin⁡U′δL∗=n′u′sin⁡U′δL′−nusin⁡UδL(2)-\frac{1}{2}S_\mathrm{I}=n'u'\sin U'\delta L^*=n'u'\sin U'\delta L'-nu\sin U\delta L\tag{2}

这个系数-1/2是后面计算式（2）结果的系数，给SIS_\mathrm{I}乘以-1/2可以消掉这个系数，有利于计算。

接下来对式（2）进行详细推导：

−12SI=n′u′sin⁡U′δL′−nusin⁡UδL=n′u′sin⁡U′(L′−l′)−nusin⁡U(L−l)=n′u′sin⁡U′(L′−r)−n′u′sin⁡U′(l′−r)−nusin⁡U(L−r)+nusin⁡U(l−r)(3)\begin{aligned} -\frac{1}{2}S_{\mathrm{I}}&=n'u'\sin U'\delta L'-nu\sin U\delta L\\ &=n'u'\sin U'(L'-l')-nu\sin U(L-l)\\ &=n'u'\sin U'(L'-r)-n'u'\sin U'(l'-r)-nu\sin U(L-r)+nu\sin U(l-r) \end{aligned}\tag{3}

这里的rr为折射球面的半径

图 4. 单个折射球面几何图

ΔHCA′\Delta HCA'中用正弦定理

L′−rsin⁡I′=rsin⁡U′⇒n′(L′−r)sin⁡U′=n′rsin⁡I′=nrsin⁡I(4)\frac{L'-r}{\sin I'}=\frac{r}{\sin U'}\Rightarrow n'(L'-r)\sin U'=n'r\sin I'=nr\sin I\tag{4}

同理对于近轴光线也满足式（4）

n′(l′−r)u′=n′ri′=nri(5)n'(l'-r)u'=n'ri'=nri\tag{5}

ΔHCA\Delta HCA中用正弦定理，则有

{n(−L+r)sin⁡(−U)=nrsin⁡In(l−r)u=nri(6)\left\{ \begin{aligned} n(-L+r)\sin (-U)&=nr\sin I\\ n(l-r)u&=nri \end{aligned} \right.\tag{6}

将式（4）（5）（6）带入式（3）

−12SI=n′u′sin⁡U′(L′−r)−n′u′sin⁡U′(l′−r)−nusin⁡U(L−r)+nusin⁡U(l−r)=nru′sin⁡I−nrisin⁡U′−nrusin⁡I+nrisin⁡U=nri(sin⁡U−sin⁡U′)+nr(u′−u)sin⁡I(7)\begin{aligned} -\frac{1}{2}S_{\mathrm{I}}&=n'u'\sin U'(L'-r)-n'u'\sin U'(l'-r)-nu\sin U(L-r)+nu\sin U(l-r)\\ &=nru'\sin I-nri\sin U'-nru\sin I+nri\sin U\\ &=nri(\sin U-\sin U')+nr(u'-u)\sin I\\ \end{aligned}\tag{7}

留意图3中的红色虚线框部分，可以得到

{u′−u=i−i′U′−U=I−I′ni=n′i′⇒ {u′+i′=u+iU′+I′=U+Ini=n′i′(8)\left\{ \begin{aligned} u'-u&=i-i'\\ U'-U&=I-I'\\ ni&=n'i' \end{aligned} \right. \qquad\Rightarrow\qquad\ \left\{ \begin{aligned} u'+i'&=u+i\\ U'+I'&=U+I\\ ni&=n'i' \end{aligned} \right. \tag{8}

所以式（7）可以表示为

−12SI=nri(sin⁡U−sin⁡U′)+nr(u′−u)sin⁡I=nri(sin⁡U−sin⁡U′)+nr(i′−i)sin⁡I=nri[(sin⁡U−sin⁡U′)+sin⁡I(1−i′i)]=nri[(sin⁡U−sin⁡U′)+sin⁡I(1−nn′)]=nri[(sin⁡U−sin⁡U′)+(sin⁡I−sin⁡I′)]=nri[(sin⁡U+sin⁡I)−(sin⁡U′+sin⁡I′)]=2nri[sin⁡U+I2cos⁡U−I2−sin⁡U′+I′2cos⁡U′−I′2]=2nrisin⁡U+I2[cos⁡U−I2−cos⁡U′−I′2](9)\begin{aligned} -\frac{1}{2}S_{\mathrm{I}}&=nri(\sin U-\sin U')+nr(u'-u)\sin I\\ &=nri(\sin U-\sin U')+nr(i'-i)\sin I\\ &=nri[(\sin U-\sin U')+\sin I(1-\frac{i'}{i})]\\ &=nri[(\sin U-\sin U')+\sin I(1-\frac{n}{n'})]\\ &=nri[(\sin U-\sin U')+(\sin I-\sin I')]\\ &=nri[(\sin U+\sin I)-(\sin U'+\sin I')]\\ &=2nri\left[\sin\frac{U+I}{2}\cos\frac{U-I}{2}-\sin\frac{U'+I'}{2}\cos\frac{U'-I'}{2}\right]\\ &=2nri\sin\frac{U+I}{2}\left[\cos\frac{U-I}{2}-\cos\frac{U'-I'}{2}\right] \end{aligned}\tag{9}

式（9）用了积化和差公式，我们还需要找到rr与LL的关系。根据图4，过O做入射光的垂线与OH构成的三角形中用正弦定理

Lsin⁡Usin⁡(π−π−U′−I′2−I)=2rsin⁡U′+I′2sin⁡π2⇒r=Lsin⁡U2sin⁡U+I2cos⁡U−I2(10)\frac{L\sin U}{\sin(\pi-\frac{\pi-U'-I'}{2}-I)}=\frac{2r\sin\frac{U'+I'}{2}}{\sin\frac{\pi}{2}}\qquad\Rightarrow\qquad r=\frac{L\sin U}{2\sin\frac{U+I}{2}\cos\frac{U-I}{2}}\tag{10}

将式（10）代入式（9）中

−12SI=2niLsin⁡U2sin⁡U+I2cos⁡U−I2sin⁡U+I2[cos⁡U−I2−cos⁡U′−I′2]=niLsin⁡Ucos⁡I−U2⋅[cos⁡U−I2−cos⁡U′−I′2]=niLsin⁡Ucos⁡I−U2⋅(−2sin⁡U−I+U′−I′4sin⁡U−I−U′+I′4)=niLsin⁡Ucos⁡I−U2⋅(−2sin⁡U−I′2sin⁡I′−I2)=niLsin⁡Ucos⁡I−U2⋅−4sin⁡U−I′2cos⁡U−I′2sin⁡I′−I2cos⁡I′−I22cos⁡U−I′2cos⁡I′−I2=−12niLsin⁡Ucos⁡I−U2⋅sin⁡(U−I′)sin⁡(I′−I)cos⁡U−I′2cos⁡I′−I2=−niLsin⁡Usin⁡(I′−U)sin⁡(I−I′)2cos⁡I−U2cos⁡I′−U2cos⁡I−I′2(11)\begin{aligned} -\frac{1}{2}S_{\mathrm{I}}&=2ni\frac{L\sin U}{2\sin\frac{U+I}{2}\cos\frac{U-I}{2}}\sin\frac{U+I}{2}\left[\cos\frac{U-I}{2}-\cos\frac{U'-I'}{2}\right]\\ &=\frac{niL\sin U}{\cos\frac{I-U}{2}}\cdot\left[\cos\frac{U-I}{2}-\cos\frac{U'-I'}{2}\right]\\ &=\frac{niL\sin U}{\cos\frac{I-U}{2}}\cdot\left(-2\sin\frac{U-I+U'-I'}{4}\sin\frac{U-I-U'+I'}{4}\right)\\ &=\frac{niL\sin U}{\cos\frac{I-U}{2}}\cdot\left(-2\sin\frac{U-I'}{2}\sin\frac{I'-I}{2}\right)\\ &=\frac{niL\sin U}{\cos\frac{I-U}{2}}\cdot\frac{-4\sin\frac{U-I'}{2}\cos\frac{U-I'}{2}\sin\frac{I'-I}{2}\cos\frac{I'-I}{2}}{2\cos\frac{U-I'}{2}\cos\frac{I'-I}{2}}\\ &=-\frac{1}{2}\frac{niL\sin U}{\cos\frac{I-U}{2}}\cdot\frac{\sin(U-I')\sin(I'-I)}{\cos\frac{U-I'}{2}\cos\frac{I'-I}{2}}\\ &=-\frac{niL\sin U\sin(I'-U)\sin(I-I')}{2\cos\frac{I-U}{2}\cos\frac{I'-U}{2}\cos\frac{I-I'}{2}} \end{aligned}\tag{11}

令所有角度都很小，用弧度代替正弦值，ll代替LL，所有余弦值为1，则有

SI=luni(i−i′)(i′−u)=hP(12)S_\mathrm{I}=luni(i-i')(i'-u)\tag{12}=hP