VPI中的全局参数
全局参数
全局参数指原理图中所有模块共有的变量。其中一些参数会被模块自动使用,而另一些,例如SampleRateDefault、BitRateDefault则必须在模块的参数列表中明确使用。
双击顶层原理图(vtmu,VPI Transmission Maker Universe)的背景来编辑全局参数。
默认比特率、时间窗口、默认采样率和最大质因数限制
首先应该考虑的四个全局变量是BitRateDefault、TimeWindow、SampleRateDefault和GreatestPrimeFactorLimit。
首先为每个信道选一个数据(比特)率BBB。
例如,设置BitRateDefault=10e9;
此参数不会传递给任何模块,需要在模块中明确将其作为参数字符串输入。
因此,在其它模块中设置BitRate=BitRateDefault;
通过这种方法令所有Tx都使用相同的比特率。
接下来要选择每个Block中要仿真的Bit数MMM。此数值与每个Bit的采样数SSS一起定义了将要生成的信号中的采样数NNN。仿真引擎允许使用任意数量的采样进行模拟,但FFT的速度取 ...
VPI中信号的表现形式
信号的表现形式
信号的表现形式定义了数据在仿真模块之间传递的形式,决定了模块所能处理的内容。
块模式和采样模式
VPI的模拟仿真中,相邻模块之间可以单向或双向传递数据,模块之间的数据交换频率通常取决于它们之间的物理时延。短时延意味着数据传递频繁,以便形成光学谐振。长时延意味着数据传递频率较低,数据以数据块的形式传递,每个数据块代表波形的一个时间窗口。
大多数系统仿真是通过在组件之间传递数据块来实现高效地执行,即表示时域或频域中信号的向量,这在VPItransmissionMaker系统中称为块模式。
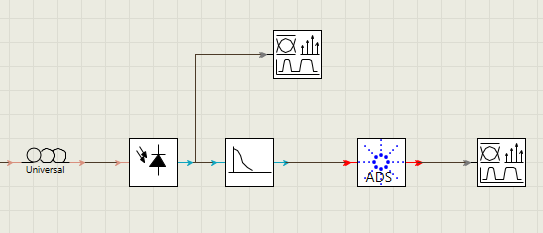
块模式下,当系统模块的输入端有数据可用时,每个模块都会触发。仿真通常会从发射端到接收端依次进行,每次一个模块,如下图所示
另一种模式为采样模式,这种模式下数据一次传递一个样本。采样模式用于组件紧密耦合且皮秒级双向交互需着重考虑的场合中,例如在光子链路和多段激光器中。VPIcomponentMaker包含许多使用采样模式的示例。
块模式内的信号表示
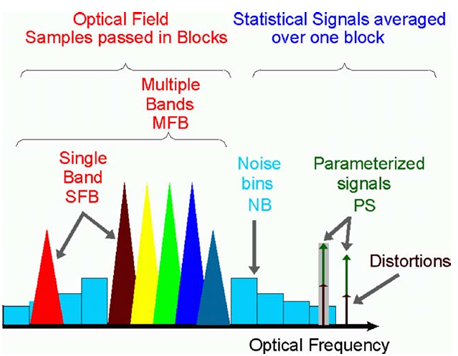
块内数据控制着信号的表现形式,它可以包含以下形式的数据
采样信号,例如光场或电压/电流,以固定时间间隔进行采样。仿真带宽取决于采样率。
...
偏振分束旋转器件(PSR)
PSR 的背景和作用
偏振分束旋转器(PSR)是解决绝缘衬底上硅(SOI)平台光波导器件偏振敏感的关键性器件,解决了偏振模色散(PMD)导致的脉冲展宽和码间干扰。偏振分束旋转器(Polarization Beam Splitter Rotator, PBSR)是一种集成了偏振分束和偏振旋转功能的光学器件,主要用于控制光束的偏振态,实现特定偏振光的分离或转换。
1. 核心功能
偏振分束(PBS功能):将入射光按偏振方向分成两束正交的线偏振光(如P光和S光),分别沿不同路径输出。
偏振旋转(旋转功能):将其中一束光的偏振方向旋转(如90°),使得两束输出光具有相同的偏振态(例如均变为P光)。
2. 工作原理
分束机制:通常基于双折射晶体(如方解石)或介质膜偏振分束立方体,利用不同偏振光折射率差异实现分束。
旋转机制:通过半波片(Half-Wave Plate)或液晶相位延迟器对选定光束的偏振方向进行旋转。
3. 典型结构
集成设计:在传统偏振分束器(PBS)的输出端口之一加入半波片,使一束光的偏振方向被旋转,而另一束保持不变。
示例:
输入光:非偏振光或任意偏振光。
分束 ...
科研人必学神器:Rmarkdown+Latex+Tikz+GeoGebra
前言
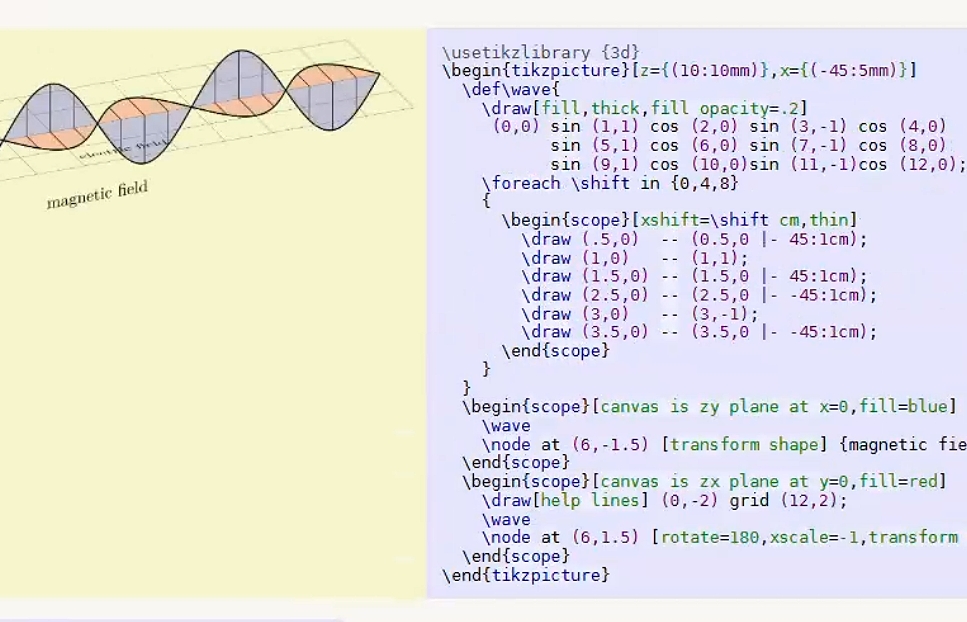
大家有没有想过,教科书上的公式是怎么写出来并排版的如此美观的呢?如何能在文档中绘制出美观而精确的科研绘图?想必绝大多数同学都只知道MS Office,但是这太Low了,而且排版格式经手多人会变得千奇百怪。科研人就要有科研人的个性,不仅要严谨,还要有科研人的专属工具,展现出科研人高大上的一面!
R + Markdown = RMarkdown
Markdown大家都知道,但凡入门了计算机的玩家都靠这个来写博客,记录知识和见闻,但知道Rmarkdown的玩家就不多了,毕竟R语言受众相对C,Java,Python而言还是太少。但身为科研工作者不能不知道它,因为R是开源的,主要用于统计分析、绘图以及数据挖掘的强大编程语言。你可能会说“我都有Python了,用个Jupyter不一样的吗? ”,但Jupyter这种人尽皆知的工具无法体现出您的与众不同,尽管Jupyter现在也能在Python3.10+的环境中结合Jupyter-Tikz来实现相同的效果,但科研人还是要多学学新工具。
Rmarkdown的使用需要基于R+Rstudio,R和Rstudio直接去官网下载就行了,独立安装即可。 ...
VPI中加载光s4p参数
VPI中加载S参数
核心思想
S参数的本质是线性传输矩阵,传输矩阵的矩阵元通过指定滤波器来描述;
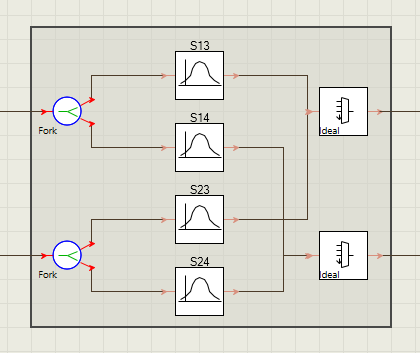
本例仅考虑s4p的前向传播矩阵元,即S13,S14,S23,S24四个参数,这是因为端口3和4仅由端口1和2的线性叠加而成 ;
用s4p参数描述X_Coupler
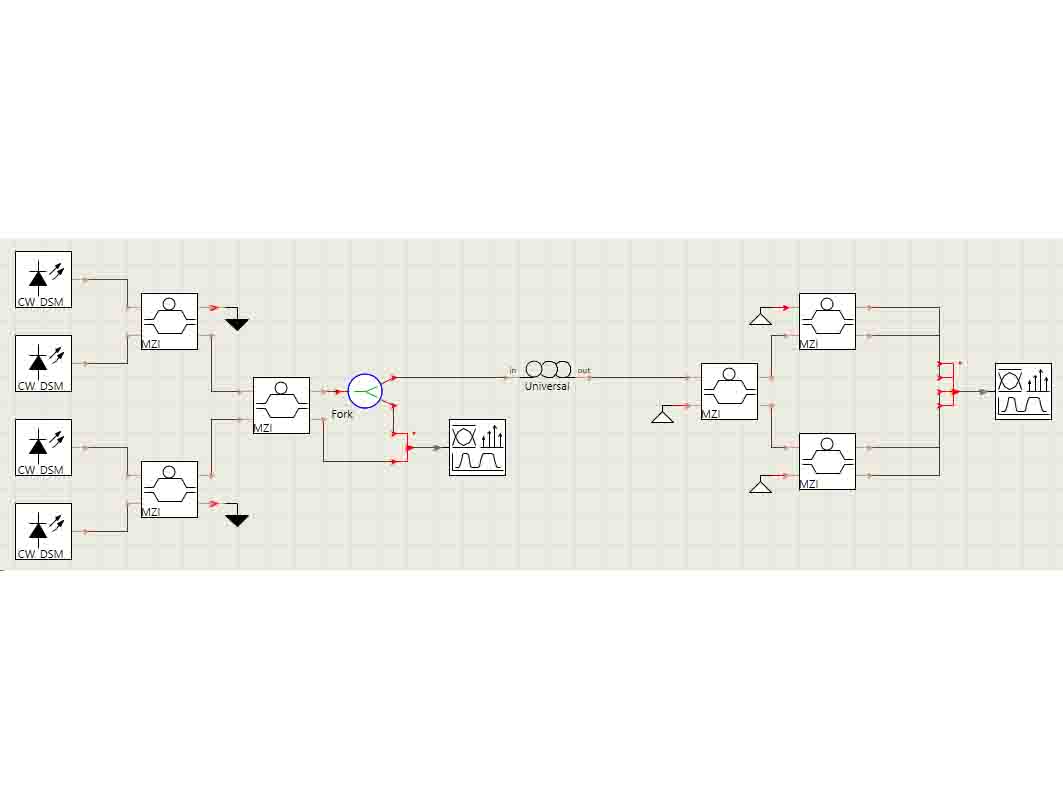
X_Coupler作为一个经典的传输模型,具有如下的传输结构
该结构仅考虑前向传输,若考虑反向传输,则需要使用S31,S41,S32,S42。双向传输需要考虑全部16个S参数。
s4p参数的导入
在VPI的FilterOpt控件中导入s4p文件需要满足如下格式
使用该格式后,需要在控件Measured Filter栏目下的DataFormat中填入Frequency Magnitude Phase。需要额外注意的是单位描述,其中Phase项的单位只有角度,而非弧度。INTERCONNECT中导出的弧度数据需要换算后方可载入。
提取INTERCONNECT中S参数的python函数如下
1234567891011121314151617181920212223242526272829303132333435363738 ...
ADS中调用VPI模块(VOL)进行联合仿真
VOL模块
注意事项
ADS中使用VOL模块需要保证:
ADS的版本为2021,VPIphotonics版本为11.1;
ADS的license中,需要有W3071E的模块,可以去License Manager里看,没有就无法使用VOL模块;
VPI的license中,需要有额外几个SED的Feature,分别是 VPI_TMM_OPTICALSYSTEMS_SED,VPI_CM_FIBERAMPLIFIER_SED,VPI_CM_ACTIVEPHOTONICS_SED 和 VPI_TMM_LAB_SED。这几个SED的Feature可以让ADS用脚本调用VPI的Engine Driver,实现无GUI的仿真计算;
VPI的vtmu中需要有两个vtmg模块,分别是ADS_Dynamic_Input 和 ADS_Dynamic_Output。该俩模块中各有一个python脚本实现ADS数据类型转换,分别是create_signal_from_file.py 和 create_file_from_signal.py。确保这四个文件到位,否则无法实现联合仿真;
VPI的python环境需新 ...
MZI 实现波分和解波分复用
MZI实现波分和解波分复用
利用MZI实现波分和解波分复用依据的理论是干涉理论,根据上下臂的相位分配可以控制输出光相干相长或相消。
对于一个X_Coupler,其传输矩阵可以写为如下形式:
T(f)=(1−αjαjα1−α)(1)T(f)=
\left(
\begin{matrix}
\sqrt{1-\alpha} & j\sqrt{\alpha}\\
j\sqrt{\alpha} & \sqrt{1-\alpha}
\end{matrix}
\right)\tag{1}
T(f)=(1−αjαjα1−α)(1)
其中α\alphaα为上臂功率占总功率的比值。
一个完整的二端口MZI复用器由两个X_Coupler组成,中间经由两路臂长不等的光路实现相位调控,总体传输矩阵可以写为如下形式:
T(f)=(1−α2jα2jα21−α2)(e−j2π(f−fc)τ001)(ejϕupper00ejϕlower)(1−α1jα1jα11−α1)(2)T(f)=
\left(
\begin{matrix}
\sqrt{1-\alpha_2} & j\sqrt{\ ...
VPI中调用ADS模块进行联合仿真
ADS 模块
注意事项
VPI中使用ADS接口模块需要保证:
ADS的版本为2021,VPIphotonics版本为11.1;
在环境变量中添加两个ADS的路径:
12<ADS installation directory>\bin<ADS installation directory>\adsptolemy\lib.win32.
如果能跑通Simulation Techniques ⇒\Rightarrow⇒ Cosimulation ⇒\Rightarrow⇒ ADS中的Demo,则表示联合仿真可行。
只跑通Demo可远远不够,需要跑通自己定义的ADS模型才算实现真正意义上的联合仿真。
创建ADS模板文件
在希望调用ADS模块vtmu工程的Input文件夹内New一个MyWorkspace,New一个Schematic。这个Schematic作为TestBench放在最顶层,同时也作为VPI与ADS的接口;
在ADS中找到TimedDataRead和TimedDataWrite两个Parts,用于VPI与ADS之间的数据传输;
在A ...
正交幅度调制 QAM
正交幅度调制QAM
正交幅度调制QAM(Quadrature Amplitude Modulation)是Wi-Fi中一种常用的数字信号调制,是相位调制与幅度调制的组合。
为了提高信号传输速率,需要让一种波形传递更多的比特信息。普通的幅度调制和相位调制仅有两种符号来区分0或1,相当于调制一次只能传递一个比特信息。但最大调制速率受到硬件限制,硬件的响应时间是存在极限的,调制太快了硬件反应不过来,因此希望通过调制编码的方式来提升单次调制下传输的比特位数。
电场的波形可以由振幅和相位表示,即复振幅。反映在复平面上的分布图即为波形星座图。QAM的星座图如下
QAM是将信号加载到两个正交载波上实现的,通过对这两个载波调整并叠加,最终得到相位和幅度都调制过的信号。这两个载波一个称为I信号,一个称为Q信号,因此这种调制方式也称为IQ调制。
信号调制分类
TDECQ 检测技术
TDECQ 检测技术
TDECQ检测技术用于评估PAM4光发射机通信质量,完整名称为“针对四相调制的发射机色散眼图闭合代价(Transmitter and Dispersion Eye Closure for PAM4(Quaternary))”。
TDECQ的背景
从NRZ信号到PAM4信号的转变需要变革测试参数和测试方法。早期评估光发射机通信质量的测试规范为发射机色散代价(Transmitter and Dispersion Penalty, TDP),最早出现于2002年发布的IEEE802.3ae中针对10GBase-SR/LR/ER的发射机指标规范中。
信息的传输需要制定规范和协议。IEEE全称Institute of Electrical and Electronics Engineers,即电气与电子工程师协会,是规范制定者们的协会,但具体制定者所在的群体是协会中某个下属层级。协会中的层级首先是顶级IEEE——协会,二级是Society——学会,三级是Committee——委员会,四级是Work Group——工作组,五级是Task Group——任务组。
IEEE80 ...